Image \(\operatorname{Im}(f)\) de l'
Application linéaire \(f:E\to F\)
Ensemble des valeurs prises par \(f\). $$\operatorname{Im}(f)=f(E)=\{f(x)\mid x\in E\}$$
- obtention : si \((x_i)_{i\in I}\) est génératrice de \(E\), alors l'image est l'Espace vectoriel engendré :$$\operatorname{Im}(f)=\operatorname{Vect}\{f(x_i)\mid i\in I\}$$
- propriété importante : \(f\) surjective \(\iff\) \(\operatorname{Im}(f)=F\)
Définition
Définition :
Soit \(f\) une application linéaire de \(E\) dans \(F\)
L'ensemble \(\{f(u):u\in E\}\), noté \(\operatorname{Im} f\), est appelé image de \(f\)
Formule
Si \(E=\operatorname{Vect}(u_1,u_2,\ldots,u_n)\), alors $${{\operatorname{Im}f}}={{\operatorname{Vect}\left(f(u_1),f(u_2),\ldots,f(u_n)\right)}}$$
(
Ensemble des combinaisons linéaires)
Propriétés
Sous-espace vectoriel
Proposition :
\(\operatorname{Im}f\) est un sous-espace vectoriel de \(E\)
(
Sous-espace vectoriel)
Démonstration :
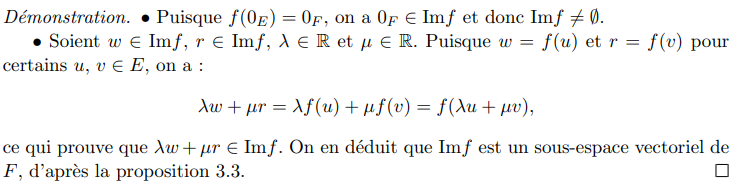
Lien avec les surjections
Proposition :
\(f\) est surjective si et seulement si \({{\operatorname{Im}f}}={{F}}\)
(
Surjection)